在程序编写中，循环和递归有着各自的优势，循环易于理解但会让问题规模扩大，递归可以炫技、清晰明了但不易阅读，且受限于大规模的数据问题。本文将对运行效率问题做一个探讨。

问题简介

本文选取了一个简单的输出“1~N”的问题，来简单探讨下递归和循环到底谁更快的问题。
为了量化比较，选用了ms为单位。

计算程序用时代码

# include <stdio.h>
# include <windows.h>
# include <time.h>
{
    long start,end,runtime;
    start = clock();
    Functions();
    end = clock();
    runtime = end - start;
}

完整程序

# include<stdio.h>
# include <windows.h>
# include <time.h>

//程序说明：两种方法输出1~N； 
//结论：递归运算速率理论上应该大于循环运算，但实际情况下因为递归对函数的多重调用，反而更慢
//且递归对于大规模运算较为吃力 

void PrintN( int N );
void PrintG( int N );

int main()
{
    int N = 0;
    long op,ed,op2,ed2;
    printf("请输入数字：");
    scanf("%d",&N);
    op = clock();
    PrintN( N );
    ed = clock();
    printf("\n");
    printf("循环程序共用时：%ldms\n",ed-op);
    op2 = clock();
    PrintG( N );
    ed2 = clock();
    printf("\n");
    printf("递归程序共用时：%ldms\n",ed2-op2);
    return 0;
}

//递归 
void PrintG( int N )
{
    if( N ){
        PrintN(N-1);
        printf("4%d ",N); 
    }
    return;
}

//循环
void PrintN( int N)
{
    for( int i=1;i<=N;i++ )
    {
        printf("%4d ",i);
    }
} 

运行结果

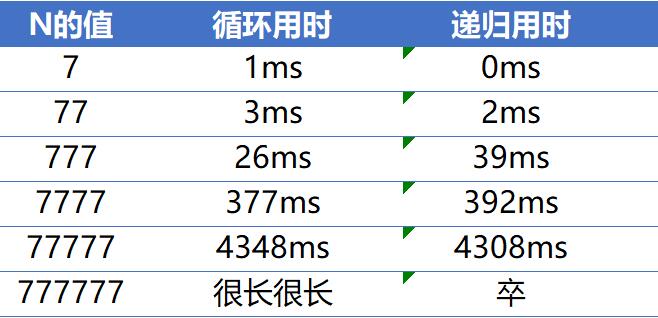
又一个例子

这次拿了数学中著名的斐波那契数列作为例子，这个例子可以明显看出循环的优势在哪里。

#include <stdio.h>
#include <windows.h>
#include <time.h>

//目的：通过斐波那契数列比较递归和循环的效率差别 
//这里的序号从0开始，即斐波那契第0项和第一项都为1 

int FibonacciDigui( int n );
int FibonacciXunhuan( int n );

int main()
{
    int n = 0;
    long op,ed,op2,ed2;
    scanf( "%d",&n );    //输入n的值
    op = clock();
    int result = FibonacciDigui(n);
    ed = clock();
    printf("递归结果是%d\n",result);
    printf("斐波那契递归程序共用时：%ldms\n",ed-op);
    op2 = clock();
    int result2 = FibonacciXunhuan(n);
    ed2 = clock();
    printf("递归结果是%d\n",result2);
    printf("斐波那契循环程序共用时：%ldms\n",ed2-op2);
    return 0;
}

int FibonacciDigui( int n )
{
    if ( n <= 1 )
        return 1;
    else
        return FibonacciDigui(n-1) + FibonacciDigui(n-2);
}

int FibonacciXunhuan( int n )
{
    int FibN = 0,Fib0 = 1, Fib1 = 1;
    if ( n<=1 )
        return 1;
    else
        for( int i=2; i<=n; i++ )
        {
            FibN = Fib0 + Fib1;
            Fib0 = Fib1;
            Fib1 = FibN;
        }
        return FibN;
}

那我们来看看运行效率对比

39
递归结果是102334155
斐波那契递归程序共用时：584ms
递归结果是102334155
斐波那契循环程序共用时：0ms

---

Process exited after 2.037 seconds with return value 0
请按任意键继续. . .

差距非常明显，而且递归处理这个问题那是相当地考研机器性能，这才第39个斐波那契而已。如果100,500,甚至更大机器八成会直接罢工掉。到了千万数量级，还要头铁用递归的话或许就只能请我国的天河二号出马来完成这个闲得蛋疼的任务了。。。

最终结论

循环方法比递归方法快, 因为循环避免了一系列函数调用和返回中所涉及到的参数传递和返回值的额外开销。
递归和循环之间的选择。一般情况下, 当循环方法比较容易找到时, 你应该避免使用递归。这在问题可以按照一个递推关系式来描述时, 是时常遇到的, 比如阶乘问题就是这种情况。
递归其实是方便了程序员难为了机器。它只要得到数学公式就能很方便的写出程序。优点就是易理解，容易编程。但递归是用栈机制实现的（c++），每深入一层，都要占去一块栈数据区域，对嵌套层数深的一些算法，递归会力不从心，空间上会以内存崩溃而告终，而且递归也带来了大量的函数调用，这也有许多额外的时间开销。所以在深度大时，它的时空性就不好了。
递归并不节省存储器的开销，因为递归调用过程中必须在某个地方维护一个存储处理值的栈。递归的执行速度并不快，但递归代码比较紧凑，并且比相应的非递归代码更易于编写与理解。在描述树等递归定义的数据结构时使用递归尤其方便。